Solució Tasca 7è lliurament
Exercici 1.
a) Observant la gràfica, les imatges demanades són:
f(1) = 4
f(2) = 0
f(0.5) = 2.7 aproximadament
b) Punts de tall de la funció amb l'eix X són:
(0 , 0) (2 , 0)
c) Punt de tall de la funció amb l'eix Y és:
(0 , 0)
d) Les coordenades del màxim i dels mínims relatius de la funció
màxim (1 , 4)
mínims (0 , 0) i (2 , 0)
e) Interval de Creixement (0,1) U (2, +∞) i Intervals de decreixement (-∞,0) U (1,2)
--------------------------------------------------------------------------
Exercici 2.
- a) Calculeu el domini de la funció f(x).
Cal estudiar cada una de les dues parts de la funció per separat i també els punts de transició d'una funció a l'altra.
Part I
|
Part II
|
Punt de transició entre la part I i la II
|
|
g(x) és una funció polinòmica de 1r grau
És una recta
No cal fer res
|
p(x) és una funció polinòmica de 2n grau
És una paràbola
No cal fer res |
En el punt x=2 hi ha imatge
f(2) = 2 2 - 1 = 3
|
| Dom g(x) = Reals | Dom p(x) = Reals | x=2 és del domini |
| Per tant Dom f(x) = Reals |
- b) Estudia la continuïtat de la funció en x= 2 i en cas que la funció sigui discontínua, digues de quin tipus.
Recordeu que una funció és contínua en un punt x0 :
Estudiarem el comportament de la funció en x=2
 | A l'esquerra de 2 li correspon la funció de la part I |
 | A a dreta de 2 li correspon la funció de la part II |
 |
Per tal que els tres valors coincideixen, cal que 2a+1 = 3 → a= 1
Per tant la funció serà contínua per a=1 i discontínua si a≠1
- c) Calcula
- d) Calcula
- e) Calculeu les imatges de x=-1 de x=1 i de x=3 i "a" pren el valor obtingut en l'apartat b
f(-1) = a(-1)+1=1(-1)+1=0
f(1) = a(1)+1=1(1)+1=2
f(3) = (3)2-1=8
- f)
Si ara a=0 la funció és :
Per saber quina és la gràfica correcta podem fer alguns càlculs com ara f(0) f(1) o altres valors
f(0) = 1
f(1) = 1
f(3) = 8
Ara mirem quina gràfica compleix amb aquestes condicions. Solament gràfica 2, per tant no cal seguir.
Resposta, la gràfica que correspon a la funció és la gràfica 2


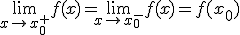


No hay comentarios:
Publicar un comentario